문제 링크: https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
풀이 및 코드
<N = 1, 3, 5, 7, 9 ...>
N이 홀수일 때는 경우의 수가 존재하지 않아 항상 0을 출력한다.
<N = 2>

위 그림과 같이 총 세가지 경우의 수가 존재한다.
<N = 4>

먼저 생각할 수 있는 경우의 수는 3 x 2 크기의 벽 두 개로 3 x 4 벽을 나타낼 수 있다는 것이다.
이렇게 되면 각 3 x 2 벽의 경우의 수는 3이고 이게 하나가 더 있으므로 3 x 3 으로 나타낼 수 있다.
이게 끝이 아니다.
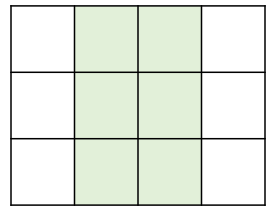
이런식으로 가운데가 이어진 부분도 생각해봐야 한다.
앞서 생각한 3 x 3 의 경우의 수는 각 3 x 2 크기의 벽 두개로 생각했기 때문에 중간이 이어진 경우의 수는 생각하지 못했다. 따라서 가운데가 이어진 부분의 경우의 수를 생각해보면,

이렇게 두 가지가 나온다.
따라서 N = 4일 때의 경우의 수는 3 ^ 2 + 2 = f(2) x 3 + 2 = 11로 나타낼 수 있다.
<N = 6>
이제부터는 어떻게 하면 앞서 구한 값들로 N = 6일 때의 경우의 수를 나타낼 수 있을지에 대해 생각해봐야 한다.
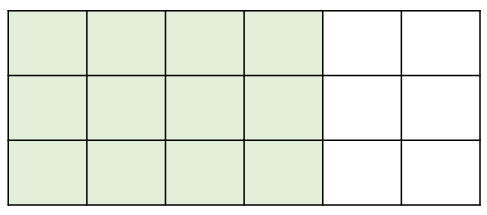
먼저, 위 그림처럼 N = 4의 경우에서 오른쪽에 3 x 2 벽이 붙었다고 생각하면 경우의 수는 f(4) x 3 = 33 이다.

위 그림의 경우에는 경우의 수가 존재하지 않는다. -> 항상 짝수개씩 생각해야 한다.

오른쪽 3 x 4가 가운데가 이어진 3 x 4라고 생각해야 한다. (떨어진 3 x 4 는 이미 첫번째 경우에 포함되었다.) 따라서 이 경우에는 앞선 3 x 2의 경우의 수 3개, 오른쪽 3 x 4가 이어졌을 때의 경우의 수 2개를 곱해 3 x 2 = 6 이다.
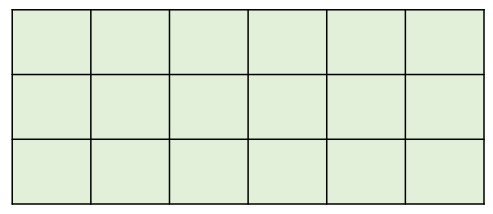
3 x 6의 벽이 모두 이어져 있다고 하면, 경우의 수는 다음과 같이 2가지가 나온다.
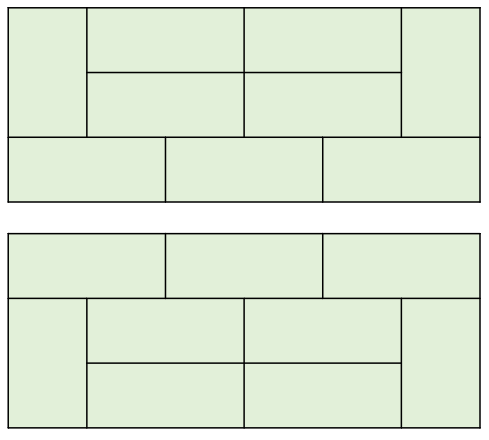
따라서 N = 6일 때의 경우의 수는 f(4) x 3 + 2 x (f(2) + 1) = 41이다.
<N=8>
N = 8일 때도 위 방법으로 해보면,
경우의 수는 f(6) x 3 + 2 x (f(4) + f(2) + 1)이다.
이 과정을 일반화하여 식으로 나타내면,
f(N) = f(N - 2) x 3 + 2 x (f(N-4) + f(N-6) + ... + 1)이 된다.
위 식을 코드로 나타내면 다음과 같다.
#include <iostream>
using namespace std;
int dp[30];
int main(){
int N;
cin >> N;
dp[0] = 0;
dp[1] = 3;
// 각 element 당 dp 값 채우기
for(int i = 2; i < N; i++){
if(i % 2 == 0) // N = 1, N = 3, N = 5 등 N이 홀수일 때 dp값 0 (index 는 짝수)
dp[i] = 0;
else{
dp[i] = dp[i - 2] * 3;
int temp = 0;
for(int j = i - 4; j > 0; j -= 2){
temp += dp[j];
}
temp += 1;
dp[i] += temp * 2;
}
}
cout << dp[N-1] << endl;
return 0;
}
https://github.com/haram1117/AlgorithmStudy/commit/2d9832c534ccdcb3ee766155d468ce4a05f6f93b
DP2133 · haram1117/AlgorithmStudy@2d9832c
Show file tree Showing 7 changed files with 44 additions and 37 deletions.
github.com
'알고리즘 > BOJ' 카테고리의 다른 글
| 알고리즘 - 백준 2193 (이친수) (0) | 2023.01.06 |
|---|---|
| 알고리즘 - 백준 2156 (포도주 시식) (1) | 2023.01.05 |
| 알고리즘 - 백준 2011 (암호코드) (0) | 2023.01.03 |
| 알고리즘 - 백준 1912 (연속합) (2) | 2023.01.03 |
| 알고리즘 - 백준 1699 (제곱수의 합) (0) | 2023.01.01 |
