이진 검색 트리 (Binary Search Tree)
이진 검색 트리는 다음과 같은 속성을 갖는 이진 트리이다.
- 부모 노드의 값 >= 왼쪽 자식 노드의 값
- 부모 노드의 값 <= 오른쪽 자식 노드의 값
이는, 부모 노드보다 작거나 같은 모든 원소는 항상 왼쪽에 있고 부모 노드보다 크거나 같은 원소는 항상 오른쪽에 있게 된다. 따라서 원소 검색을 위해 루트 노드부터 차례대로 값을 비교하는 경우, 각 단계마다 검색 범위가 절반으로 줄어든다.
BST가 마지막 레벨을 제외한 모든 노드에 두 개의 자식 노드가 있으면 BST의 검색 및 삽입 동작은 O(logN)의 시간복잡도를 갖는다. 이러한 형태의 이진 트리는 완전 이진 트리라고 한다.
BST에서 원소 검색
이진 검색 트리에서 원소를 검색할 때는 이진 검색 트리의 특징을 이용해 검색 범위를 반으로 줄이면서 수행할 수 있다.
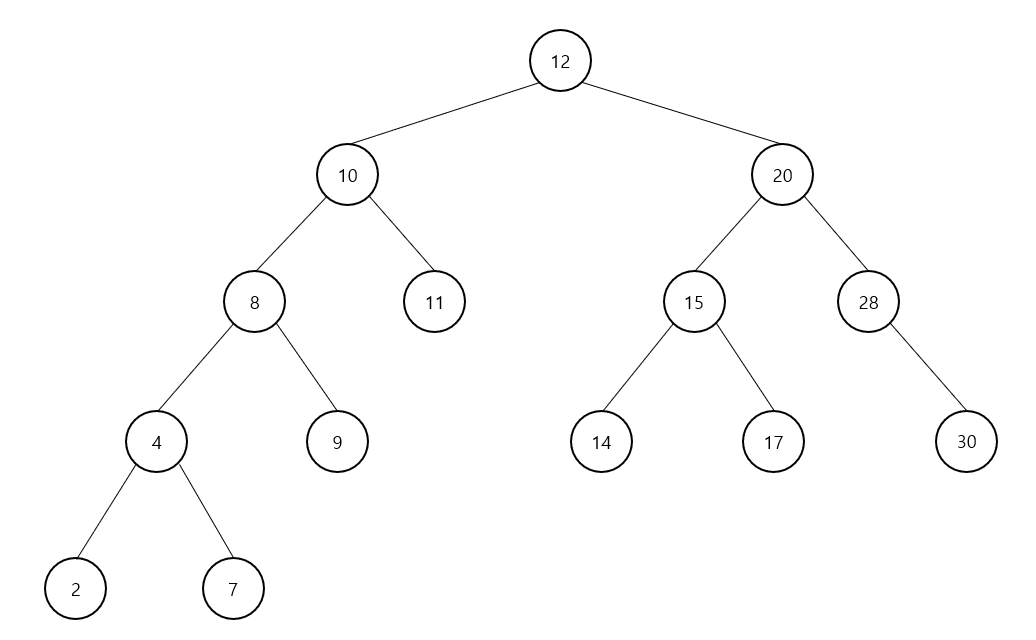
위 그림과 같은 BST에서 숫자 7을 검색하기 위해 각 노드에서 어느 하위 노드로 이동할 지 정해야 한다.
루트 노드 (12)와 7을 비교하면 7이 더 작기 때문에 왼쪽 하위 노드로 이동한다.
이 후 10과 7을 또 비교하면 7이 더 작으므로 왼쪽 하위 노드로 이동하고, 이를 반복하여 4와 7을 비교하여 오른쪽 하위 노드로 이동한 후 숫자 7을 찾을 수 있다.
이러한 방식으로 현재 노드가 찾고자 하는 노드가 아닐 때마다 검색 범위가 반으로 줄어든다.
BST에 새 원소 삽입

위 그림과 같이 구성되어 있는 BST에서 숫자 18을 삽입하려면 어떻게 해야 할까?
새로운 원소를 추가하려면 먼저 원소가 삽입될 위치의 부모 노드를 찾아야 한다. 이는 원소 검색과 비슷한 방식으로 이루어진다.
12 < 18, 20 > 18, 15 < 18, 17 < 18 이기 때문에

위 그림처럼 17의 오른쪽 하위노드에 18이 삽입된다.
BST에서 원소 삭제하기
BST에서 원소를 삭제할 때에는 단순히 노드를 삭제하는 것 뿐만 아니라, 노드 삭제 후 전체 트리가 BST 속성을 만족하도록 해야 한다.
이를 위해서 첫 번째단계로 삭제할 노드를 찾는다. 이후에는 해당 노드의 자식 노드에 따라 수행할 행동이 달라지게 된다.
1) 삭제할 노드의 자식 노드가 없는 경우: 단순히 해당 노드를 삭제하면 된다.
2) 삭제할 노드의 자식 노드가 하나인 경우: 노드 삭제 후, 부모 노드의 포인터가 해당 자식 노드를 가리키도록 조정한다.
3) 삭제할 노드의 자식 노드가 두 개 있는 경우: 노드 삭제 후, 현재 노드를 후속 노드로 대체한다.
여기서 1번과 2번은 크게 복잡하지 않지만, 3번은 추가 작업이 필요하다.
3번의 후속노드란, 현재 노드 다음으로 큰 숫자를 가진 노드를 말한다. (현재 원소보다 큰 원소들 중에 가장 작은 원소)
그렇기 때문에, 이 후속노드를 찾기 위해서는 서브 트리에서 가장 왼쪽에 위치한 노드로 이동하면 된다.

위와 같은 BST에서 12를 삭제하고 싶을 때, 앞에 설명한 대로 노드 삭제 후, 현재 노드를 후속 노드로 대체하는 작업이 필요하다.
그러기 위해서는 먼저 '후속 노드'를 찾아야 한다.
후속 노드는 현재 노드(12) 보다 큰 값을 가진 노드 중 가장 작은 값을 가진 노드를 의마하기 때문에 12의 오른쪽 서브 트리에서 가장 왼쪽에 위치한 노드를 찾으면 된다.
위 BST에서 후속 노드는 15가 될 것이다.
그 후에는, 후속 노드 값을 루트 노드에 복사한다.

그 후에는 원래 후속 노드를 삭제해주어야 한다.
이 삭제 또한 앞에 서술한 과정과 동일하게 적용한다.
이 때, 후속 노드는 항상 오른쪽 자식 노드만 갖게 될 것이다. 만약 왼쪽 노드에 값이 존재했다면, 해당 후속 노드보다 작은 값이 서브 트리에 존재했다는 의미이므로 후속 노드가 올바르지 않다는 의미이다.
그래서 결국 해당 후속 노드까지 삭제하면,

위 그림과 같이 12가 삭제된 BST가 될 것이다.
시간 복잡도
트리 연산의 시간복잡도는 이론적으로는 매번 검색 범위가 반 씩 줄어들기 때문에 $ O(logN) $ 이다.
그러나, BST는 트리의 모양이 삽입 순서에 따라 달라진다는 점, 검색 범위가 항상 n/2씩 줄어든다는 것도 보장할 수 없기 때문에 시간 복잡도 $ O(logN) $이 항상 정확하다고 볼 수 없다.
균형 트리에서 조금 더 정확하게 시간 복잡도를 계산하는 방법을 다뤄보려 한다.
'알고리즘 > 알고리즘 공부' 카테고리의 다른 글
| [2. 트리, 힙, 그래프] 힙 (1) | 2023.03.14 |
|---|---|
| [2. 트리, 힙, 그래프] 균형 트리, n항 트리 (0) | 2023.02.15 |
| [2. 트리, 힙, 그래프] 트리 (1) | 2023.01.18 |
| [1. 리스트, 스택, 큐] 컨테이너 어댑터 (0) | 2023.01.17 |
| [1. 리스트, 스택, 큐] C++ std::deque (0) | 2023.01.15 |
