반응형
선형 자료 구조로 표현할 수 없는 대표적인 문제로 계층적 문제(hierarchical problem)와 순환 종속성(cyclic dependency) 문제가 있다.
회사의 조직도, 대학의 교과 과정 계층도 등은 계층적으로 데이터를 표현해야 한다. 이 때 사용하는 자료 구조는 트리 (tree)이다.

위 그림처럼 트리는 계층을 구성한다. 데이터가 저장된 부분은 노드(node)라고 부르고, 노드와 노드 사이를 잇는 선을 edge라고 부른다.
가장 맨 위에 나타나는 노드를 root node라고 한다.
트리의 기본 구조에 대한 요약이었고, 트리의 원소를 순회하는 방법은 세 가지로 나뉜다.
전위 순회 (preorder traversal)
이 방법은 현재 노드를 먼저 방문하고, 그 다음은 현재 노드의 왼쪽 하위 노드를, 마지막으로는 현재 노드의 오른쪽 하위 노드를 재귀적인 방식으로 방문한다.

preorder 방식을 코드로 구현하면 다음과 같이 구현할 수 있다.
static void preOrder(node* start)
{
if(!start)
return;
cout << start->position << ", ";
preOrder(start->first);
preOrder(start->second);
}
중위 순회 (in-order traversal)
중위 순회 방법은 왼쪽 노드를 먼저 방문하고, 현재 노드, 오른쪽 노드를 방문한다.
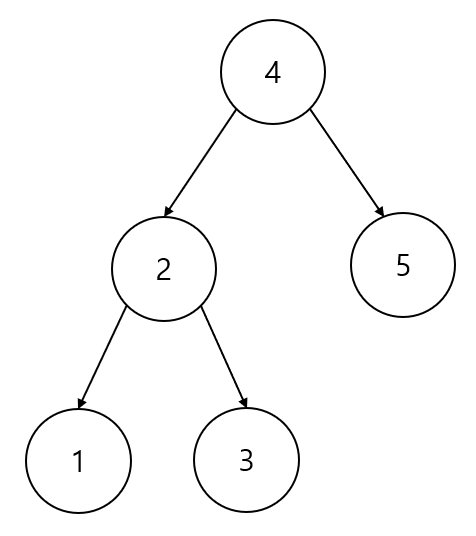
in-order 방식을 코드로 구현하면 다음과 같다.
static void inOrder(node* start)
{
if(!start)
return;
inOrder(start->first);
cout << start->position << ", ";
inOrder(start->second);
}
후위 순회 (post-order traversal)
이 방법은 두 자식 노드를 먼저 방문한 후, 현재 노드를 방문한다.
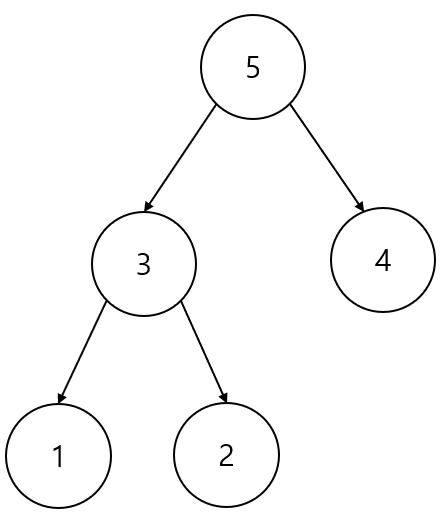
post-order 방식을 코드로 구현하면 다음과 같다.
static void postOrder(node* start)
{
if(!start)
return;
postOrder(start->first);
postOrder(start->second);
cout << start->position << ", ";
}
레벨 순서 순회 (level order traversal)
트리의 맨 위 레벨부터 아래 레벨까지, 왼쪽 노드에서 오른쪽 노드 순서로 방문한다.
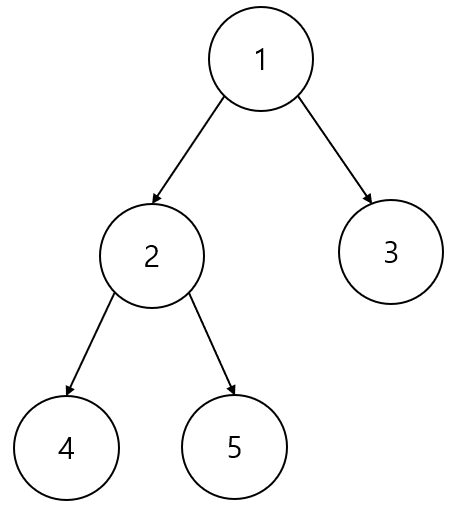
레벨 순서 순회는 다음 코드와 같이 작성할 수 있다.
static void levelOrder(node* start){
if(!start)
return;
queue<node*> q;
q.push(start);
while (!q.empty()){
int size = q.size();
for(int i = 0; i < size; i++){
auto current = q.front();
q.pop();
cout << current->position << ", ";
if(current->first)
q.push(current->first);
if(current->second)
q.push(current->second);
}
cout << "\n";
}
}반응형
'알고리즘 > 알고리즘 공부' 카테고리의 다른 글
| [2. 트리, 힙, 그래프] 균형 트리, n항 트리 (0) | 2023.02.15 |
|---|---|
| [2. 트리, 힙, 그래프] 이진 검색 트리(Binary Search Tree) (0) | 2023.02.15 |
| [1. 리스트, 스택, 큐] 컨테이너 어댑터 (0) | 2023.01.17 |
| [1. 리스트, 스택, 큐] C++ std::deque (0) | 2023.01.15 |
| [1. 리스트, 스택, 큐] C++ std::list (0) | 2023.01.15 |
